秘密共享：隐私计算与区块链共识中的榫卯

本文转载自：Secret Sharing - Mortise and Tenon in Privacy Computing and Blockchain Consensus
原文发布日期：2021年8月17日
来源：绿盟科技博客
作者：吕亮

一、引言

2018年5月正式生效的GDPR是欧盟“史上最严”条例，是数十年来数据安全和数据隐私法规方面最重要的一次变化。随后，2019年生效的加州CCPA，对个人数据及信息保护提出了严格的界定和保护要求。至此，GDPR和CCPA对欧美国家在数据安全和隐私行业的立法产生了持续的影响。在我国，2021年6月10日，中华人民共和国第十三届全国人民代表大会常务委员会第二十九次会议正式表决通过了《中华人民共和国数据安全法》。历经三次审议和修改通过的《数据安全法》将于2021年9月1日正式施行。在数据安全和隐私保护方面，企业合规性是一个迫在眉睫的事情。

随着对数据安全和隐私保护的重视和相关法案的出台，各种数据拥有者重新回到数据孤岛的状态。为了实现数据的可用不可见技术并使得互联网公司在合规下能利用大数据和AI技术做更多有意义的事情。在这个背景下，相应的互联网公司提出了一系列的解决方案，如：谷歌的联邦学习、腾讯微众的联邦学习、阿里的共享学习。其中，腾讯微众的联邦学习主要采用了同态加密。谷歌的联邦学习和阿里的共享学习则使用了秘密共享技术，这反映了对秘密共享的算法研究有着重要的意义。

纵观区块链的发展脉络，其经历了初始的1.0阶段，发展成熟的2.0阶段，即将进入新的发展阶段。其吞吐率和挖矿资源浪费问题一是阻碍区块链发展的瓶颈。如何突破这一瓶颈，去中心化的区块链共识算法的突破是核心。运用秘密共享技术的应用去探索去中心化区块链共识算法的突破有很实际的意义。

本文通过对秘密共享技术的介绍和思考，进一步探讨秘密共享的根源以及秘密共享在数据安全和区块链共识等领域的应用。

二、秘密共享

秘密共享（Secret Sharing，SS）是1979年由Shamir和Blakey提出的，并在此之后40多年秘密共享被广泛认识和深入的研究。

秘密共享著名的(t，n)阈值方案如图1所示：设秘密s被分成n个部分，每一部分被称为一个子秘密并由一个持有者持有，并且大于等于t个参与者所持有的子秘密可以重构(Reconstruction)秘密s，而少于t个参与者所持有的子秘密无法重构秘密并且无法获得秘密s的任何信息。

秘密共享方案的三种实现技术：

基于超平面几何的秘密共享，包括Blakley方案和Brickell方案； 基于插值多项式的秘密共享，包括经典的Shamir阈值秘密共享方案； Mignotte，Asmuth & Bloom提出的基于中国剩余定理的秘密共享； 基于中国剩余定理的秘密共享是在环上的运算，而Blakley & Brickell的超平面几何秘密共享方案和Shamir阈值秘密共享方案是在有限域上的运算，所以基于中国剩余定理的秘密共享和其他两个秘密共享的理论基础不尽一样。鉴于此，本文暂未讨论中国剩余定理。以下内容主要探讨前两者技术，通过分析方案的结构对两者的关系进行了统一，总结了Shamir秘密共享的优点。

2.1 Blakley和Brickell的超平面几何方案 Blakley通过多维欧几里得空间来构造阈值秘密共享机制。任何t非平行t-1维超几何平面在一个t维空间中交易一点。秘密通过编码在坐标中完成秘密共享。如图3所示的三维欧几里得空间中的三个平面交与一点，秘密可以嵌入到交点的某一个坐标中。Blakley方案的秘密分发和秘密重构过程如下：

秘密分发：构造n个t维空间中的t-1维超几何平面分发给n个参与者，其中n>=t；图2是一个3维空间中的2维平面生成，一个秘密拥有者Dealer通过空间中的一个已知点P（秘密s是P的一个坐标值）的条件下生成任意多个过该点的平面。

秘密重构：n个参与者中的t个参与者可以重构秘密s。如图3：任意3个参与者即可实现对共享点（包含秘密s）的重构，即三个非平行平面的交点。

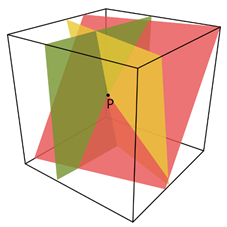
在秘密共享方案中，信息率是度量秘密共享方案安全性和效率的一个重要指标。所谓秘密共享的信息率可以简单理解为秘密的信息规模与每个子秘密的信息规模的比率。Brickell的向量方法（矢量方法）相比于Blakley超平面几何的方法能够有效提高信息率。

Brickell的秘密共享方案采用向量方法，一个秘密拥有者Dealer把秘密s嵌入到一个向量中，在通过一个矩阵把秘密共享为n个子秘密分发给n个参与者，具体方法如下：

选择秘密s，和随机向量\((y_2,y_3, \ldots, y_t)\), 生成一个\(n \times t\)矩阵M，M有n行，每行记为\(M_i\),任意t个行向量都是线性无关的。秘密份额为\((s_1，s_2，\ldots，s_n)\).每个份额是行向量\(M_i\)和列向量\((s,y_2,y_3, \ldots, y_t)\)的乘积。即\(s_i = M_i \cdot (s,y_2,y_3, \ldots, y_t)^T\)

其中M是一个公开参数任何一个参与者的子秘密为\(s_i\)，任意t个参与者对应矩阵M的t个行向量，这t个向量组成一个\(t \times t\)的方阵，根据前面的要求任意t个行向量线性无关所以此方阵满秩，所以可以有效的求解到\((\omega_1，\omega_2，\ldots，\omega_t)\)使得：

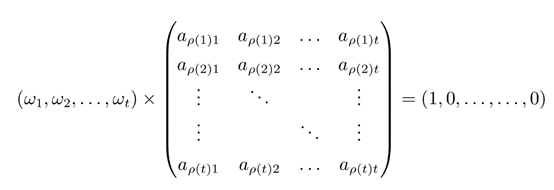
也就是任意t个M矩阵的行向量可以张成\((1,0,\ldots，0)\)然后通过如下计算可以重构s：

$$s = \sum_{i=1}^t \omega_i s_i$$

2.2 Shamir的阈值秘密共享方案

Shamir秘密共享是目前应用最为广泛的阈值秘密共享技术。Shamir秘密共享优点有哪些，它与Blakly & Brickell秘密共享的关系又是如何呢？

Shamir的方案的秘密分发和秘密重构过程如下：

秘密分发：

一个Dealer要共享一个秘密s，分给n个参与者，其中任意t个参与者可以重构秘密s，寻找一个t-1次多项式：

$$f(x) = a_0 + a_1 x + a_2 x^2 + \ldots + a_{t-1} x^{t-1}$$

其中\(a_0=s\)，Dealer为每一个参与者任意选择非0的\(x_i\)计算\(s_i=f(x_i)\)，把\(s_i\)作为子秘密发送给参与者i.

秘密重构：

任何大于等于t个参与者通过其子秘密\(s_i\)和\(x_i\)通过拉格朗日插值定理可以恢复上面多项式\(f(x)\)，并且令\(x=0\)实现秘密s的重构：

$$f(0) = \sum_{i=1}^t s_i \prod_{j=1,j\neq i}^t \frac{x_j}{x_j - x_i} = s$$

进一步对Shamir秘密分享过程进行分析，可以发现在秘密分享阶段的计算：

$$ \begin{pmatrix} s_1\ s_2\ \dots\ s_n \end{pmatrix} = \begin{pmatrix} 1 & x_1 & x_1^2 & \ldots & x_1^{t-1} \\ 1 & x_2 & x_2^2 & \ldots & x_2^{t-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \ldots & x_n^{t-1} \\ \end{pmatrix} \begin{pmatrix} a_0\ a_1\ \dots\ a_{t-1} \end{pmatrix} $$

把以上的多项式用线性方程组的视角打开来看，是一个范德蒙德矩阵和一个列向量\((a0,a_1\ldots，a{t-1})\)的乘积。其中范德蒙德矩阵和Brickell方案中的矩阵M是对应的：

$$ V = \begin{pmatrix} 1 & x_1 & x_1^2 & \ldots & x_1^{t-1} \\ 1 & x_2 & x_2^2 & \ldots & x_2^{t-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \ldots & x_n^{t-1} \end{pmatrix} $$

因此，Shamir秘密共享是Blakley & Brickell方案中的特例。正因为范德蒙德矩阵的特殊性，线性无关性（\(x_i\)不相等的任意t阶方阵都是满秩的）和构造简单（并且分布式节点很容易统一这个矩阵），所以大多数方案应用Shamir秘密共享。如果需要把Shamir秘密秘密共享应用到一般模式可以考虑把范德蒙德矩阵用一般矩阵替代。

三、可验证的秘密共享

3.1 可验证秘密共享

在秘密共享中，为了解决参与者想验证Dealer是否欺骗自己以及Dealer如何证明自己没有欺骗参与者的问题，提出了可验证的秘密共享（Verifiable Secret Sharing，VSS）。Feldman VSS 是一种基于Shamir秘密共享构造的可验证秘密共享方案。

Dealer要共享一个秘密s，分给n个参与者，其中任意t个参与者可以重构秘密s，寻找一个t-1次多项式：

$$f(x) = a_0 + a_1 x + a_2 x^2 + \ldots + a_{t-1} x^{t-1}$$

其中\(a_0=s\)，Dealer为每一个参与者任意选择非0的\(x_i\)计算\(s_i=f(x_i)\)为i的子秘密发送给参与者i.同时，Dealer计算\(A_j=g^{a_j}\),其中\(j=0，1，2\ldots，t-1\)并公开这些参数。

参与者收到秘密\(s_i\)后验证\(s_i\)的有效性，即通过验证以下等式是否成立：

$$g^{s_i} = \prod_{j=0}^{t-1} A_j^{x_i^j}$$

其中\(A_j=g^{a_j}\).

3.2 分布式可验证秘密共享

在以上所有的方案中Dealer是一个知道秘密的实体。Joint Feldman VSS.方案既能实现上述的可验证的秘密共享又能去掉Dealer。一种无可信第三方的可验证秘密共享方案（Distributed Verifiable Secret Sharing，DVSS）

具体过程如下： 每一个参与者\(P_i\)选择要共享的秘密\(s_i=a_0\)并随机选择其他参数生成\(t-1\)次多项式：

$$f_i(x) = a_0 + a_{1i} x + a_{2i} x^2 + \ldots + a_{(t-1)i} x^{t-1}$$

公开参数\(A_{ik}\)并公布，对每一参与者\(P_j\)生成秘密\(s_i\)的子秘密\(s*{ij}=f*i(x_j)\)，将\(s*{ij}\)发送给参与者\(P_j\). 每一个参与者可以验证其他参与者发送给自己的秘密是否有效，并把所有验证通过的参与者记为集合Q； 所有参与者把秘密分享验证通过集合Q内的子秘密进行加运算就得到该参与者的子秘密\(s_i\)。

四、在区块链共识和隐私保护中的应用

被称为革命性的第三代加密货币的Cardano（ADA）的共识算法Ouroboros和致力于利用区块链打造一款具备无限扩容能力的自治分布式云计算网络项目Dfinity中的共识算法都不约而同的选择了分布式可验证的秘密共享技术。在信任环境、分布式结构上，区块链的共识节点和分布式可验证秘密的参与者都恰分的对应。这样分布式可验证秘密共享的特征在区块链共识中得到充分的展现，能恰到好处的解决区块链共识算法的吞吐率和资源浪费的问题。

在日趋严格的隐私保护政策下，各种隐私保护算法被提出，其中联邦学习和共享学习最为突出，其内部的安全层都有采用了秘密共享技术实现隐私保护的技术方案。在联邦学习中，基于秘密共享的逻辑回归模型中利用了秘密共享的加法同态性，数据拥有者将秘密共享给多方，在秘密共享的场景下，将明文的计算转换为子秘密的计算，实现了隐私保护。蚂蚁金服的共享学习框架中也采用秘密共享技术作为隐私保护实现的技术之一。

五、总结

本文简要地描述了秘密共享在区块链共识和联邦学习等方面的应用，重点介绍了Blakley和Brickell的超平面几何方案、Shamir秘密共享、可验证的秘密共享和分布式可验证的秘密共享算法。另外，通过应用场景的改变进一步分析了可验证秘密共享和分布式可验证秘密共享。通过对这些秘密共享的深入分析，能够更好地理解其在区块链共识和联邦学习、共享学习的应用。

参考文献

[1] Beimel, A., Secure Schemes for Secret Sharing and Key Distribution. phd thesis israel institute of technology technion, 1996.

[2] Ito, M., et al., Secret sharing scheme realizing general access structure. Electronics and Communications in Japan (Part III Fundamental Electronic Science), 1989. 72(9): p. 56-64.

[3] Shamir, A., how to share a secret. 1979.

[4] Blakley, G.R. Safeguarding cryptographic keys (PDF). in 1979 International Workshop on Managing Requirements Knowledge. 1979.